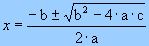Video função quadrática

Função quadrática no nosso dia-a-dia

Um exemplo de função quadrática no nosso dia-a-dia, é você sentado no ônibus, jogando um chaveiro para cima e pegando de volta na mão.
Embora para você o chaveiro só vá para cima e para baixo, quem está de fora do ônibus consegue ver o chaveiro fazer um movimento de parábola (com concavidade para baixo), pois o ônibus se movimenta para frente; além do chaveiro ir para cima.

Vídeo ensinando um pouco

http://www.youtube.com/watch?v=uWOz4GB36GQ
Créditos: MrJorgeKrung

Aqui tem alguns exercícios para vocês resolverem de função quadrática

) Em cada um dos itens abaixo, ache o vértice, o eixo de simetria do gráfico e a imagem de cada uma das funções. Classifique o vértice como um ponto de máximo ou de mínimo da função dada.
(a)
(b)
(c)

(d)
(e)
(f)


Respostas


Exercício 2


Escreva cada uma das funções abaixo na forma padrão. Esboce o gráfico de cada uma delas identificando o vértice e o eixo de simetria.
(a)
(b)


Respostas

Exercício 3


Em cada um dos itens abaixo, use o discriminante para decidir o número de vezes em que o gráfico da função corta o eixo x .
(a)
(b)
(c)


Respostas

Exercício 4


Use a fórmula de Bhaskara para resolver as equações abaixo:
(a)
(b)
(c)


Respostas

Exercício 5


(a) Calcule o valor de m na equação de modo que uma de suas raízes seja 2.

(b) Calcule o valor de m na equação de modo que uma raiz seja o triplo da outra.

Respostas

Exercício 6


1) Em cada um dos itens abaixo, escreva as funções abaixo na forma fatorada, explicitando os pontos onde o gráfico da função intercepta o eixo x . Em cada caso encontre também as coordenadas do vértice da parábola.
(a)
(b)
(c)

(d)
(e) G(x) = 13 - x2
(f)


Respostas

2) A partir da experiência adquirida na resolução do item anterior, responda:

(a) Como as raízes da equação f( x ) = 0 estão relacionadas com os pontos onde o gráfico da função intercepta o eixo x ?


(b) Como o vértice de cada uma das parábolas acima está relacionado com as raízes da equação f( x ) = 0?

Respostas

3) Suponha que o gráfico de uma função quadrática intercepte o eixo x em (-2,0) e (8,0). Ache as coordenadas do vértice do gráfico desta função.


Respostas

Exercício 7


1) Resolva as seguintes inequações do segundo grau.
(a)
(b) > 0

(c)
(d)


Respostas

Problema 1


Em relação ao problema de estamparia de camisetas apresentado na Seção Motivação deste capítulo, o lucro mensal (ou prejuízo) L, obtido com a venda de x camisetas, era dado por L( x ) = - 0,005 + 13 x -1250. Use os conhecimentos adquiridos até aqui para encontrar o número de camisetas que devem ser vendidas para que o lucro obtido seja máximo.

Respostas

Problema 2


Ainda em relação ao problema da estamparia de camisetas, apresentado na Seção Motivação deste capítulo, vimos que o preço de vendas de x camisetas deverá ser fixado em reais por camiseta.

(a) Quantas camisetas deverão ser vendidas para que a renda obtida com estas vendas seja máxima?

(b) Este mesmo nível de vendas gerará um lucro máximo?

Respostas

Problema 3


Um fazendeiro tem 100 metros de arame para delimitar um curral de forma retangular. Quais as dimensões do curral para que a área cercada seja máxima?

Respostas

Problema 4


Suponha que o fazendeiro do problema anterior, decida construir o curral com aproveitamento da parede de um celeiro, de modo a cercar apenas três lados. Se x é o comprimento de um lado perpendicular à parede do celeiro, ache a área cercada como função de x . Qual o valor de x para que a área cercada seja máxima? Qual o valor da área máxima?

Respostas

Problema 5


Uma companhia de avião freta um avião de 50 lugares de acordo com as seguintes condições especificadas no contrato de afretamento:

(i) Cada passageiro pagará R$ 600,00 se todos os 50 lugares forem vendidos.

(ii) Cada passageiro pagará um adicional de R$ 30,00 por lugar não vendido.

Quantos lugares a companhia deverá vender para obter um lucro máximo?

Respostas

Problema 6


A água que está esguichando de um bocal mantido horizontalmente a 4 metros acima do solo descreve uma curva parabólica com o vértice no bocal. Se a corrente de água desce 1 metro medido na vertical nos primeiros 10 metros de movimento horizontal, a que distância horizontal do bocal irá atingir o solo?

Respostas

Problema 7


Considere um segmento AB de medida s . Diz-se que um ponto C , entre A e B , divide o segmento em média e extrema razão se . Esta divisão também é chamada de divisão áurea e o segmento AC é dito o segmento áureo ou seção áurea de AB. O número definido pelas razões (iguais) acima é denotado pela letra grega j e é chamado número áureo ou número de ouro. Desse modo, temos que j = .

(a) Se x é o comprimento do segmento AC , mostre que x é solução da equação .

A figura abaixo ilustra o método geométrico, usado por Euclides, para dividir um segmento em média e extrema razão.


Clique aqui para entender melhor esta construção.
(b) Sabendo que ABDE é um quadrado de lado s , F é ponto médio de AE , a medida do segmento FD é igual a medida do segmento FG , e que a medida do segmento GE é igual a medida do segmento AC , mostre que a construção de Euclides está correta.

(c) Um retângulo áureo é aquele cuja altura (lado menor) tem a medida do segmento áureo da base. Este tipo de retângulo tem sido considerado por artistas e arquitetos como o retângulo mais bem proporcionado e de grande valor estético. Na figura ao lado, prove que os retângulos EDHG e ABHG são áureos.

Link: [URL=http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/capitulos/cap103.html]Aqui[/URL]

Irei postar uma introdução e um pouco do nosso próximo assunto
Função Quadrática

Definição

Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0.
Vejamos alguns exemplos de função quadráticas:
f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
f(x) = x2 -1, onde a = 1, b = 0 e c = -1
f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
f(x) = -4x2, onde a = - 4, b = 0 e c = 0



Gráfico

O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a 0, é uma curva chamada parábola.

Exemplo:

Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.x y
-3 6
-2 2
-1 0

0 0
1 2
2 6




Observação:

Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:


se a > 0, a parábola tem a concavidade voltada para cima;


se a < 0, a parábola tem a concavidade voltada para baixo;



Zero e Equação do 2º Grau

Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a 0, os números reais x tais que f(x) = 0.

  Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:



Temos:



Observação

A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando , chamado discriminante, a saber:


quando é positivo, há duas raízes reais e distintas;


quando é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);


quando é negativo, não há raiz real.

Bem pessoal irei postar alguns diagramas para um melhor entendimento de uma Função Afim
Que é a função que estamos estudando atualmente

Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é:



O gráfico de uma função afim é uma reta não perpendicular ao eixo Ox.


Domínio: D = R
Imagem: Im = R

Oooi pessoal!! Estava dando uma olhada sobre nosso assunto atual que é função afim e achei que vocês iam gostar de praticar um pouco,porque matemática é a prática, acessem esse link http://paraiso.ifto.edu.br/docente/admin/upload/docs_upload/material_b61331521e.pdf  e resolvam essas questões... Espero que gostem ;)

Função Afim

Antes de qualquer coisa temos que saber o que venha a ser função, sabemos que função é uma relação de dois valores, por exemplo: f(x) = y, sendo que x e y são valores, onde x é o domínio da função (a função está dependendo dele) e y é um valor que depende do valor de x sendo a imagem da função.

Existe vários tipos de função e hoje vamos falar da função “Afim”.

Bom, o que venha a ser “Função Afim”?

•  Definição:

Uma função f: IR → IR (f de IR em IR) chama-se função afim quando existem dois números reais a e b tal que f(x) = ax + b, para todo x є IR.

• Vejamos alguns exemplos:

1) f(x) = 6x + 5 , onde a = 6 e b = 5

2) f(x) = -x + 4 , onde a = -1 e b = 4

3) f(x) = 10x , onde a = 10 e b = 0

4) f(x) =  -9 , onde a = 0 e b = -9

5) f(x) = -4 + 7x , onde a = 7 e b = -4

• Valor de uma função afim

Na função afim f(x) = 10x + 3, podemos determinar:

1. f(1) = 10 • 1 +3 = 10 + 3 = 13. Logo, f(1) = 13.
2.  f(-2) = 10 (-2) + 3 = - 20 + 3 = -17. Logo, f(-2)= -17
3. f(-8) = 10 (-8) + 3 = - 80 + 3 = -77. Logo, f(-8) = -77